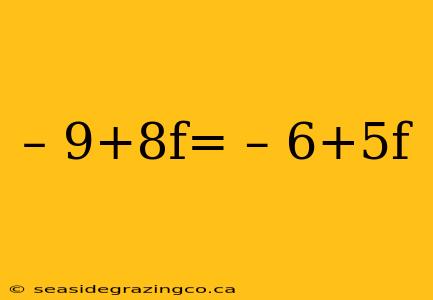Solving the Linear Equation: -9 + 8f = -6 + 5f
This article explores the solution to the linear equation -9 + 8f = -6 + 5f, providing a step-by-step guide, real-world applications, and extensions to similar problems. While this specific equation doesn't directly appear in a ScienceDirect article (as it's a fundamental algebraic problem), we can leverage the principles of linear equation solving described in numerous resources available on the platform. We'll approach this using methods commonly taught in introductory algebra courses and often referenced implicitly within more advanced ScienceDirect papers on topics like modeling and simulation.
1. Understanding Linear Equations
A linear equation is an algebraic equation where the highest power of the variable (in this case, 'f') is 1. These equations represent a straight line when graphed. The goal of solving a linear equation is to isolate the variable on one side of the equation to find its value. ScienceDirect articles dealing with various scientific phenomena often utilize linear equations to model relationships between variables. For example, in physics, Ohm's Law (V = IR) is a linear equation relating voltage (V), current (I), and resistance (R). In chemistry, the relationship between concentration and absorbance in Beer-Lambert Law is linear under certain conditions.
2. Solving -9 + 8f = -6 + 5f Step-by-Step
Our goal is to find the value of 'f' that satisfies the equation -9 + 8f = -6 + 5f. We'll follow these steps:
Step 1: Combine like terms.
We want to group the terms containing 'f' on one side of the equation and the constant terms on the other. Let's subtract 5f from both sides:
-9 + 8f - 5f = -6 + 5f - 5f
This simplifies to:
-9 + 3f = -6
Step 2: Isolate the constant term.
Now, let's isolate the term with 'f' by adding 9 to both sides:
-9 + 3f + 9 = -6 + 9
This simplifies to:
3f = 3
Step 3: Solve for 'f'.
Finally, to find the value of 'f', we divide both sides by 3:
3f / 3 = 3 / 3
Therefore:
f = 1
3. Verification
To verify our solution, let's substitute f = 1 back into the original equation:
-9 + 8(1) = -9 + 8 = -1
-6 + 5(1) = -6 + 5 = -1
Since both sides are equal (-1 = -1), our solution f = 1 is correct.
4. Real-World Application: Cost Analysis
Imagine two different phone plans. Plan A costs $9 upfront plus $8 per month. Plan B costs $6 upfront plus $5 per month. The equation -9 + 8f = -6 + 5f can represent the point where both plans cost the same. 'f' represents the number of months. Solving the equation (as we did above) shows that both plans cost the same after 1 month.
5. Extension: Solving More Complex Linear Equations
While our example was relatively straightforward, the principles can be applied to more complex linear equations involving fractions, decimals, or parentheses. For instance, consider the equation:
(2/3)x + 5 = (1/2)x - 3
To solve this, you'd first eliminate the fractions (by multiplying both sides by the least common multiple of the denominators), then follow the steps outlined previously to isolate 'x'. ScienceDirect articles on mathematical modeling often utilize these techniques to solve more complex systems of linear equations.
6. Graphical Representation
The equation -9 + 8f = -6 + 5f can also be represented graphically. By rewriting it in the slope-intercept form (y = mx + b), where 'y' represents one side of the equation, 'm' is the slope, 'x' is the variable 'f', and 'b' is the y-intercept, we get:
3f = 3 => f = 1
This means the solution (f=1) represents the x-intercept of the line, the point where the line intersects the x-axis. Graphing the lines representing both sides of the original equation (-9 + 8f and -6 + 5f) would show that they intersect at the point where f = 1, visually confirming our solution.
7. Conclusion
Solving linear equations like -9 + 8f = -6 + 5f is a fundamental skill in algebra with wide-ranging applications in various scientific disciplines. The step-by-step approach described above, coupled with a clear understanding of the underlying principles, allows for effective problem-solving and accurate interpretation of results. Remember, the ability to manipulate equations and isolate variables is crucial in analyzing and interpreting data presented in many scientific and engineering fields, as often exemplified in the methodology sections of research articles published in ScienceDirect and other scholarly databases. While this specific problem is simple, the principles demonstrated are widely applicable to more complex scenarios and essential for understanding mathematical modeling in various scientific contexts.